Today I was scrolling my phone and procrastinating as usual. I watched some tug-of-war videos and was very amazed by how people are addicted to this seemingly childish game (me included).
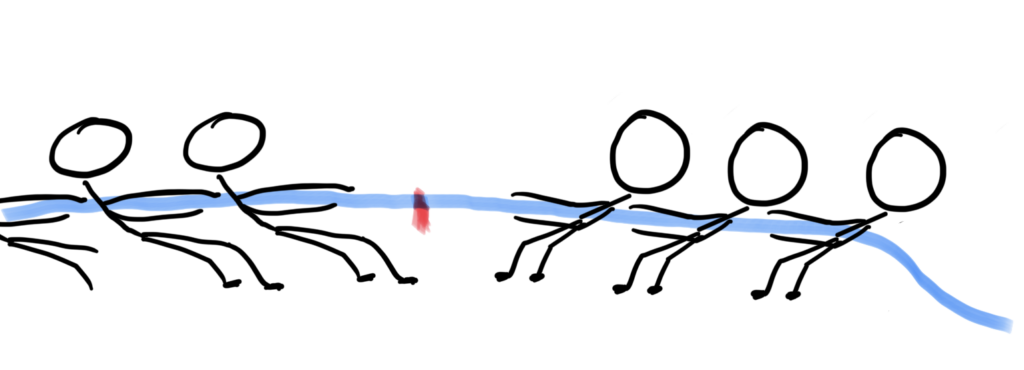
I wondered, why would they bend their body so low that their bottoms almost touched the ground? Then the boring physicist inside me woke up and said: let’s do a careful analysis of this.

By kindergarten physics(and kindergarten drawing) we know that the forces are balanced, meaning that N=G, F=f, so F_{max}=f{max}=\mu mg. However, we can maximise the force by increasing the pressure exerted on the ground, like this
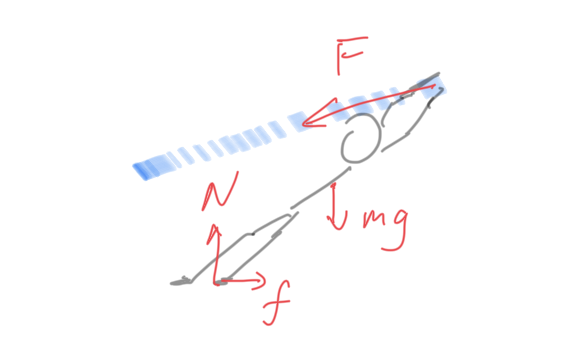
Some force from the rope helps against the ground, therefore the maximum friction is increased; the same analysis goes on the other side. In conclusion, if you hold your part of the rope higher, it will give you an advantage and your opponents’ disadvantage.
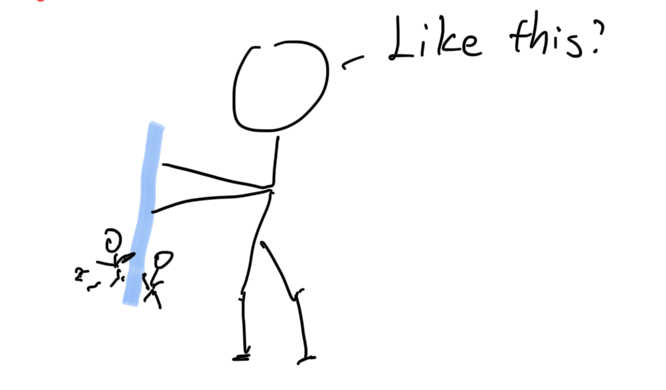
Uhhhhh….. probably?
Of course this doesn’t happen in real life, at lease(hopefully) you have not seen any tug-of-war like this.
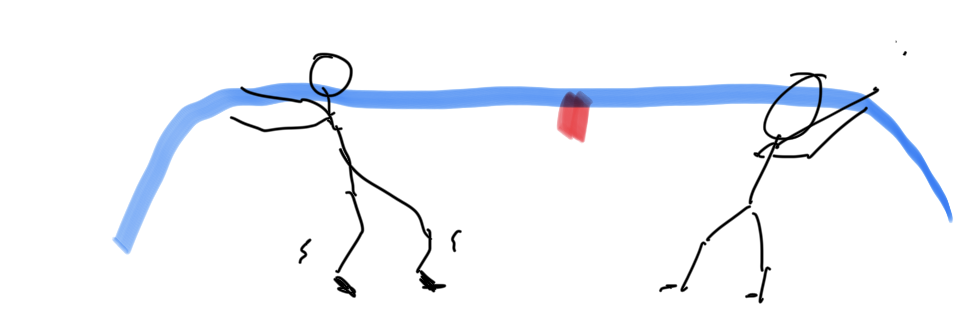
This is probably because the frictional constant is quite big and is usually not the key factor. The rubber shoes they put on have a large frictional constant, which has to do with van der Waals force.
That being said, what we should consider is the stability around your feet.
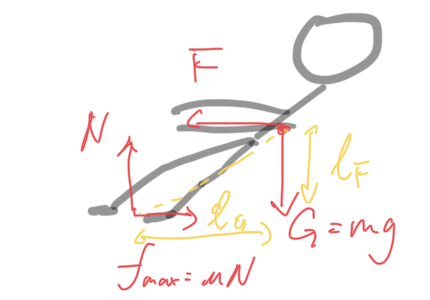
What actually makes you lose is not that you’re sliding on the floor, but you are imbalanced and rotating around your feet. In this aspect, the maximum force is F=mg * l_G / l_F. To lower your centre of gravity is to reduce l_F, therefore it makes sense to lower the body, instead of holding your hands upright to try pulling your opponents up like the way you pull out giant white radishes.
