Disclaimer: the blog is motivated from a mathematics point of view. I apologise for my lack of computer graphic knowledge and please point it out if you spot anything suspicious.
I. Rotations and translations
Rotations in real life are everywhere. You may constantly rotate a pen between your fingers. Or a fidget. Or a magical flying saucer. However, in a computer, rotation may not be so easy. You have to calculate each pixel’s location after the rotation and store the data somewhere.
There is a way of doing 90 degrees rotation by iterations of translation.
input(image)
list segments=[image]
while 1
divide each segment image into 4 pieces
translation according to figure 1
subdivide each segment, add to new_segments
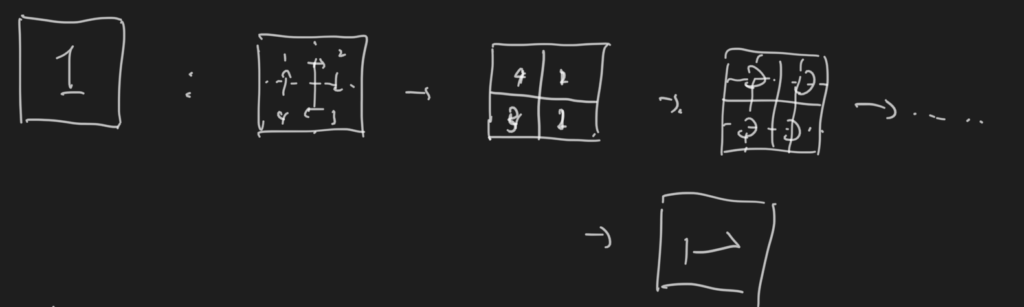
It is an exercise for the reader to execute the program in any language they prefer and verify.
But why?
[Proofs alert]
II The power of Coding
Let’s first see how that works in the 1D case.
Claim: For a 1D line, when we perform the following infinite numbers of translations:

It corresponds to a 180 degrees flip.
Proof: Imagine the line is a [0,1] interval. For each iteration of translation, we cut the segment in half and swap the two. For the centre point of the original segment, it stays where it is. These points correspond to values of m/2^n, where m and n are natural numbers. It can be shown that these points are taken care of. The rest are the points that don’t terminate.
We can map each point in the line to an infinitely long list of binary numbers. If the point is on the left-hand side of the segment, the digit is 0. Otherwise, it is 1. For example, 0.3 would correspond to (010011…). In fact, (0.010011…) is the binary representation of 0.3.
What do infinitely many translations correspond to? For the first operation, it flips the first digit; the second operation flips the second one; and so on. We say the new number would be the bit-flip of the original number, and for each digit, the two always add to 1. In binary representation, (0.111111…)_2=1 (By the way, this is an example of Leibniz equality which goes deep into the Category Theory).
For the [0,1] segment, two numbers adding up to 1 means that they are each other’s image after a mirror symmetry, which is the same as a 180 degrees rotation!
Remark. The number of points in [0,1] is the same as the real numbers. The map between the points in [0,1] and an infinitely long series of binary numbers is saying 2^N=R. Cantor’s Theory then easily shows that real numbers are uncountable.
We will use a similar coding system to complete our proof in the 2D case.
proof. denote R as rotation operation for each segment, T as segmentations and translation operation within the new segments. Therefore, we only need to prove T(T(T….)…)=R, i.e. for any x in the square, R(x)=lim_{n->\infty}T^n(x)
For a point x, we have |R(x)-T^n(x)|<1/2^(n-1)(why?), so the Euclidean distance is decreasing to 0.
III Generalisation 1: Other rotation angles?
How far can this method lead us? What rotation angles can we achieve?
The next easiest grid is a triangle lattice, and we can achieve 120 degrees:

Similarly, we can rotate by 60 degrees: a hexagonal shape can be rotated by sub-deviding them into triangles and performing translations.
How about other angles? It seems like we are dealing with fractals, and I have no idea how to deal with them.
IV Generalisation 2: Other dimensions?-A graph theory question
Really, what is a rotation? It corresponds to a mapping between the points. For a rotation of the form 360 degrees *m/n, we can find a finite cycle for certain points. E.g., a process of 90 degrees corresponds to the 4 vertices of the square mapping each other by 1->2->3->4->1. For other rotations, the cycle is infinitely long.
We will study the case of (hyper)cubes in this section. To make it resemble a rotation, we enforce one more condition: every two nodes of the loop must be adjacent to one another(so that the distance would not change). For example, LHS below would not be considered a valid “rotation” translation since 2 and 3 are not adjacent. [Still this is weaker condition than a rotation: the distance between two block may change]

In 1D it is easy: the unique cycle is 1->2->1. Since the length is 2, the rotation group is Z_2 and it corresponds to 180 degrees rotation.
In 2D, we can use brute force and say that the only possible arrangement is the RHS of the above graph.
The three-dimensional case is trickier. Convince yourself(or contact me if I’m wrong) that below is the only legal arrangement.
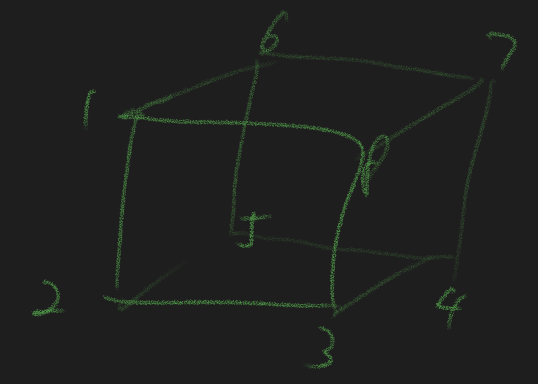
It is very tempting to conclude that there exists a unique “hyperrotation” from iterative translation in all dimensions, but the 4D case will prove it wrong. There are at least 2 non-isomorphic arrangements.
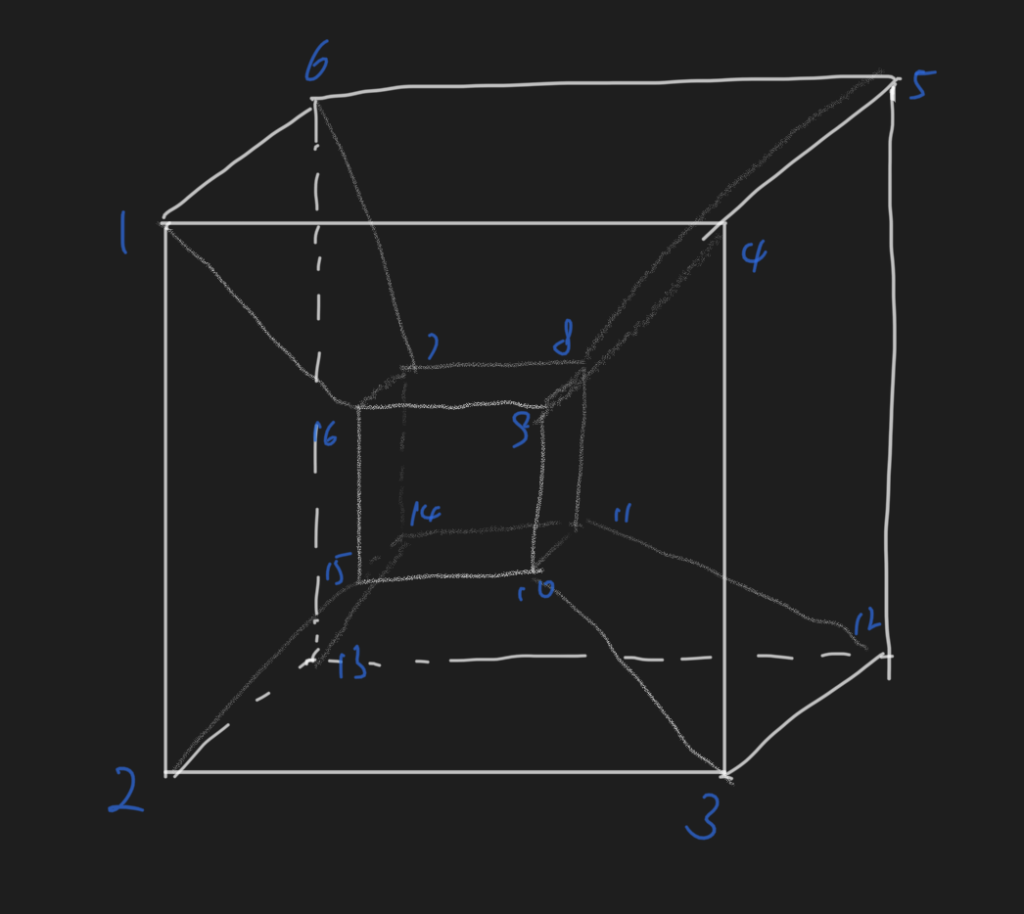
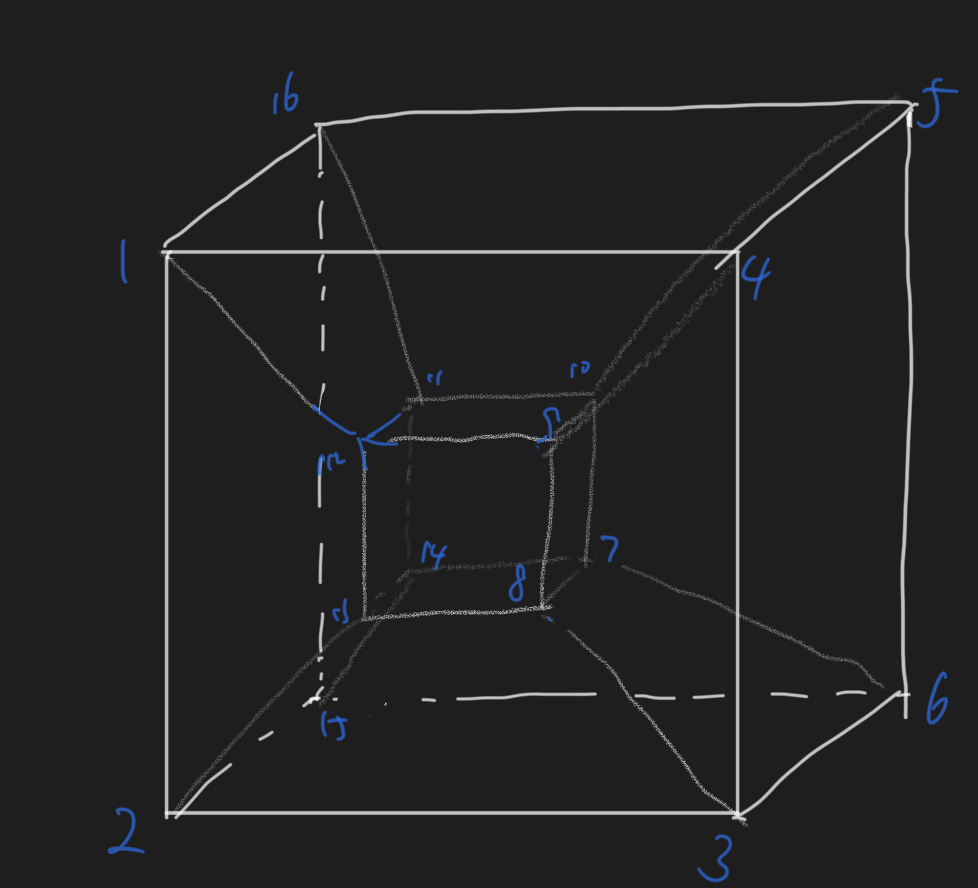
How many distinct “hyperrotation”? What happens in higher dimensions? What does the limiting process of such translation mean? What happens to other Platonian-like objects? I don’t know.
But I do know that math is a very broad subject and different parts of mathematics are connected elegantly.